Exploring Gauge-Higgs Inflation with Extra Dimensions: U(1) Gauge Theory on a Warped Background
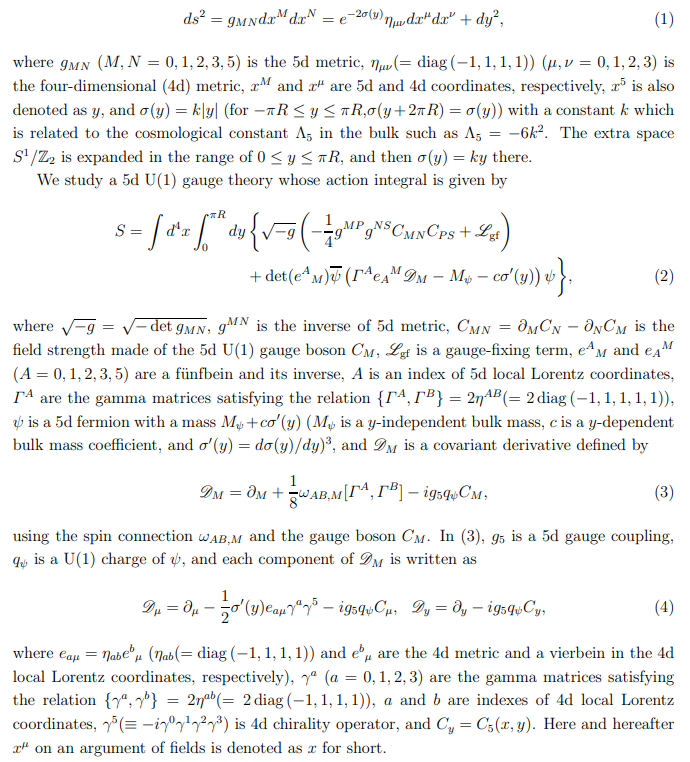
:::info
Authors:
(1) Toshiki Kawai, Department of Physics, Hokkaido University, Sapporo 060-0810, Japan (E-mail: [email protected]);
(2) Yoshiharu Kawamura, Department of Physics, Shinshu University, Matsumoto 390-8621, Japan (E-mail: [email protected]).
:::
Table of Links
Abstract and 1 Introduction
2 U(1) gauge theory on a warped background
3 Gauge-Higgs inflation on a warped background
4 Conclusions and discussions, Acknowledgements, and References
2 U(1) gauge theory on a warped background
2.1 Randall-Sundrum metric and action integral
The spacetime is assumed to be 5d one with the RS metric given by [8, 9]
\
2.2 Conjugate boundary conditions
\
where β is a constant called a twisted phase, the superscript C denotes a 4d charge conjugation, θC is a real number, and the asterisk means the complex conjugation. Then, the covariant derivatives obey the relations:
\
2.3 Mass spectrum
\
Then, the action integral is rewritten as
\
\
\
2.4 Effective potential
Let us derive the effective potential for the Wilson line phase θ(= θ(x)). Taking the standard procedure, a d-dimensional effective potential involving one degree of freedom at the one-loop level is given b
\
\
\
:::info
This paper is available on arxiv under CC BY 4.0 DEED license.
:::
[3] We introduce both Mψ and cσ′ (y) in a general standpoint, and we will see that cσ′ (y) is forbidden by imposing specific boundary conditions on fields in the next subsection.
Welcome to Billionaire Club Co LLC, your gateway to a brand-new social media experience! Sign up today and dive into over 10,000 fresh daily articles and videos curated just for your enjoyment. Enjoy the ad free experience, unlimited content interactions, and get that coveted blue check verification—all for just $1 a month!
Account Frozen
Your account is frozen. You can still view content but cannot interact with it.
Please go to your settings to update your account status.
Open Profile Settings