Deriving an Approximate Formula for Dirichlet L-Functions
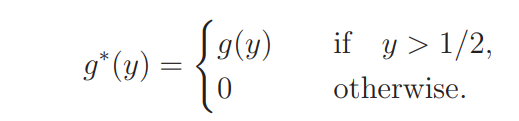
:::info
Author:
(1) Yitang Zhang.
:::
Table of Links
Abstract & Introduction
Notation and outline of the proof
The set Ψ1
Zeros of L(s, ψ)L(s, χψ) in Ω
Some analytic lemmas
Approximate formula for L(s, ψ)
Mean value formula I
Evaluation of Ξ11
Evaluation of Ξ12
Proof of Proposition 2.4
Proof of Proposition 2.6
Evaluation of Ξ15
Approximation to Ξ14
Mean value formula II
Evaluation of Φ1
Evaluation of Φ2
Evaluation of Φ3
Proof of Proposition 2.5
Appendix A. Some Euler products
Appendix B. Some arithmetic sums
References
6. Approximate formula for L(s, ψ)
Write
\
\
Let
\
\
Lemma 6.1. Suppose ψ(mod p) ∈ Ψ, |σ − 1/2| < 2α and |t − 2πt0| < L1 + 2. Then
\
L(s, ψ) = K(s, ψ) + Z(s, ψ)N(1 − s, ψ¯) + O(E1(s, ψ)),
\
where
\
\
and where
\
\
Proof. By (4.3) we have
\
\
The left side above is, by moving the line of integration to u = −1, equal to
\
\
It therefore suffices to show that
\
\
For u = −1 we have, by the functional equation (2.2) with θ = ψ,
\
\
We first show that
\
\
We move the contour of integration in (6.2) to the vertical segments
\
\
and
\
\
with the horizontal connecting segments
\
\
\
whence (6.2) follows. The proof of (6.1) is therefore reduced to showing that
\
\
:::info
This paper is available on arxiv under CC 4.0 license.
:::
\
Welcome to Billionaire Club Co LLC, your gateway to a brand-new social media experience! Sign up today and dive into over 10,000 fresh daily articles and videos curated just for your enjoyment. Enjoy the ad free experience, unlimited content interactions, and get that coveted blue check verification—all for just $1 a month!
Account Frozen
Your account is frozen. You can still view content but cannot interact with it.
Please go to your settings to update your account status.
Open Profile Settings