Deriving the DPO Objective Under the Plackett-Luce Model
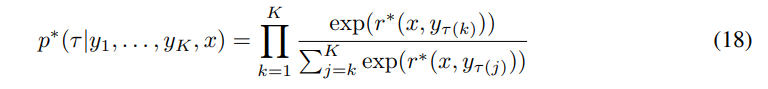
:::info
Authors:
(1) Rafael Rafailo, Stanford University and Equal contribution; more junior authors listed earlier;
(2) Archit Sharma, Stanford University and Equal contribution; more junior authors listed earlier;
(3) Eric Mitchel, Stanford University and Equal contribution; more junior authors listed earlier;
(4) Stefano Ermon, CZ Biohub;
(5) Christopher D. Manning, Stanford University;
(6) Chelsea Finn, Stanford University.
:::
Table of Links
Abstract and 1. Introduction
2 Related Work
3 Preliminaries
4 Direct Preference Optimization
5 Theoretical Analysis of DPO
6 Experiments
7 Discussion, Acknowledgements, and References
Author Contributions
\
A Mathematical Derivations
A.1 Deriving the Optimum of the KL-Constrained Reward Maximization Objective
A.2 Deriving the DPO Objective Under the Bradley-Terry Model
A.3 Deriving the DPO Objective Under the Plackett-Luce Model
A.4 Deriving the Gradient of the DPO Objective and A.5 Proof of Lemma 1 and 2
A.6 Proof of Theorem 1
\
B DPO Implementation Details and Hyperparameters
\
C Further Details on the Experimental Set-Up and C.1 IMDb Sentiment Experiment and Baseline Details
C.2 GPT-4 prompts for computing summarization and dialogue win rates
C.3 Unlikelihood baseline
\
D Additional Empirical Results
D.1 Performance of Best of N baseline for Various N and D.2 Sample Responses and GPT-4 Judgments
D.3 Human study details
A.3 Deriving the DPO Objective Under the Plackett-Luce Model
The Plackett-Luce model [30, 21] is a generalization of the Bradley-Terry model over rankings (rather than just pair-wise comparisons). Similar to to the Bradley-Terry model, it stipulates that when presented with a set of possible choices, people prefer a choice with probability proportional to the value of some latent reward function for that choice. In our context, when presented with a prompt x and a set of K answers y1, . . . , yK a user would output a permutation τ : [K] → [K], giving their ranking of the answers. The Plackett-Luce model stipulates that
\
\
Notice that when K = 2, Equation 18 reduces to the Bradley-Terry model. However, for the general Plackett-Luce model, we can still utilize the results of Eq. 5 and substitute the reward function parameterized by its optimal policy. Similarly to Appendix A.2, the normalization constant Z(x) cancels out and we’re left with:
\
\
:::info
This paper is available on arxiv under CC BY-NC-ND 4.0 DEED license.
:::
\
Welcome to Billionaire Club Co LLC, your gateway to a brand-new social media experience! Sign up today and dive into over 10,000 fresh daily articles and videos curated just for your enjoyment. Enjoy the ad free experience, unlimited content interactions, and get that coveted blue check verification—all for just $1 a month!
Account Frozen
Your account is frozen. You can still view content but cannot interact with it.
Please go to your settings to update your account status.
Open Profile Settings