Evaluating Φ1: Integrating Lemmas, Propositions, and Mellin Transforms
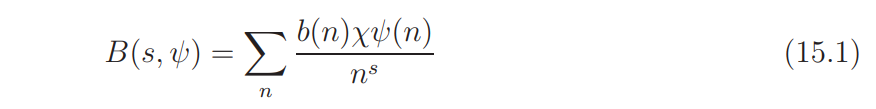
:::info
Author:
(1) Yitang Zhang.
:::
Table of Links
Abstract & Introduction
Notation and outline of the proof
The set Ψ1
Zeros of L(s, ψ)L(s, χψ) in Ω
Some analytic lemmas
Approximate formula for L(s, ψ)
Mean value formula I
Evaluation of Ξ11
Evaluation of Ξ12
Proof of Proposition 2.4
Proof of Proposition 2.6
Evaluation of Ξ15
Approximation to Ξ14
Mean value formula II
Evaluation of Φ1
Evaluation of Φ2
Evaluation of Φ3
Proof of Proposition 2.5
Appendix A. Some Euler products
Appendix B. Some arithmetic sums
References
15. Evaluation of Φ1
Recall that Φ1 is given by (13.8). In view of (12.2), B(s, ψ) can be written as
\
\
with
\
\
Write
\
\
\
where
\
\
Hence
\
\
First we prove that
\
\
Since
\
\
\
it follows that
\
\
This yields (15.4).
\
Let κ1(m) be given by
\
\
Regarding b as an arithmetic function, for σ > 1 we have
\
\
On the other hand, we can write
\
\
with
\
\
It follows by (15.3)-(15.5) and Proposition 14.1 that
\
\
where
\
\
The innermost sum above is, by the Mellin transform, equal to
\
\
where
\
\
This yields
\
\
Hence
\
\
where
\
\
On substituting n = mk we can writ
\
\
with
\
\
Hence
\
\
it follows that
\
\
If (q, dl) = 1, then
\
\
so that
\
\
for σ > 9/10. In case (q, dl) > 1 and σ > 9/10, the left side above is trivially
\
\
It follows that the function
\
\
is analytic and it satisfies
\
\
for σ > 9/10. The right side of (15.14) can be rewritten as
\
\
\
The following lemma will be proved in Appendix B.
\
\
By (15.19)-(15.21) and Lemma 15.1 we obtain
\
\
This yields, by (15.21),
\
\
To apply (15.22) we need two lemmas which will be proved in Appendix A.
\
Lemma 15.2. If |s − 1| < 5α, then
\
\
Lemma 15.3. For σ ≥ 9/10 the function
\
\
is analytic and bounded. Further we have
\
\
By (4.2) and (4.3),
\
\
By Lemma 15.3, we can move the contour of integration in the same way as in the proof of Lemma 8.4 to obtain
\
\
This together with Lemma 15.2 and 15.3 yields
\
\
since
\
\
It follows by (15.22) that
\
\
By Lemma 5.8,
\
\
Hence, by direct calculation,
\
\
Combining these relations with (15.23) , (15.17) and (15.6) we conclude
\
\
:::info
This paper is available on arxiv under CC 4.0 license.
:::
\
Welcome to Billionaire Club Co LLC, your gateway to a brand-new social media experience! Sign up today and dive into over 10,000 fresh daily articles and videos curated just for your enjoyment. Enjoy the ad free experience, unlimited content interactions, and get that coveted blue check verification—all for just $1 a month!
Account Frozen
Your account is frozen. You can still view content but cannot interact with it.
Please go to your settings to update your account status.
Open Profile Settings